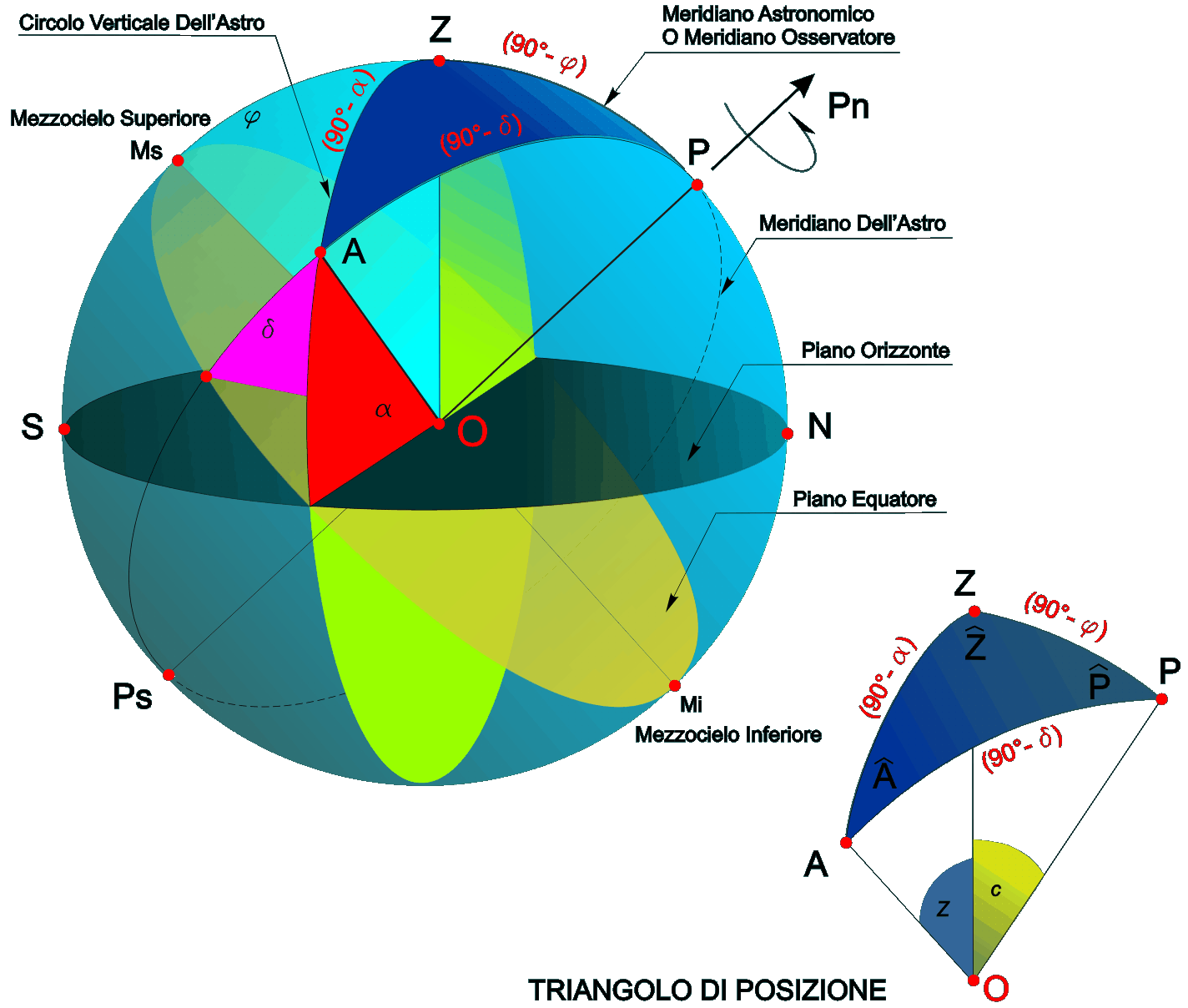
| Triangolo Sferio Il triangolo sferico è la superficie sulla sfera limitata da tre archi di circoli massimi. I piani che contengono i circoli formano fra di loro angoli diedri che corrispondono agli angoli che le tangenti formano ai vertici. Triangolo Di Posizione Il triangolo di posizione è la superficie del triangolo sferico posto sulla sfera celeste limitata da tre archi di circoli massimi passanti per l'osservatore (O) posto su un punto qualsiasi della superficie terrestre. I piani che contengono i circoli formano fra di loro angoli diedri che corrispondono agli angoli che le tangenti formano ai vertici A (astro), Z (zenit) e P (polo). Formula Di Eulero Definizione: In un triangolo sferico il coseno di un lato (cos z) è uguale al prodotto dei coseni degli altri due (cosc; cosp), più il prodotto dei loro seni moltiplicato per il coseno dell'angolo fra essi compreso (senc; senp; cosw). Dove w è l'angolo Orario. 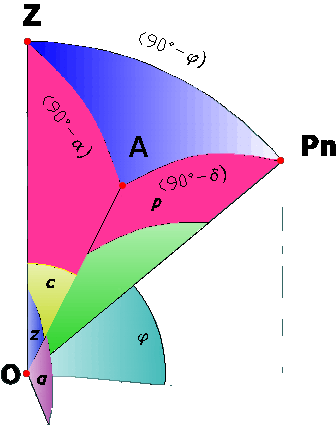
|
 |
| Dimostrazione: Calcolo Altezza (a) e Distanza Zenitale (z): Per dimostrare questo affascinante teorema si fa uso del triangolo sferico di posizione di un generico astro A (sole) sulla sfera celeste. Il Triangolo sferico di posizione può essere definito da qualsiasi orizzonte dove è posto l' osservatore (O) sulla superficie terrestre attraverso i seguenti parametri: Indicando con c=(90°-f); p=(90°-d); z=(90°-a) gli angoli complementari sottesi ai lati di un triangolo sferico e con: f = latitudine; d = Declinazione; a = Altezza del sole Si considera un piano (п ) ortogonale all'asse polare O-Pn e si scompone il triedro sferico di posizione su un piano ortogonale a п passante per OD, come sotto illustrato. * 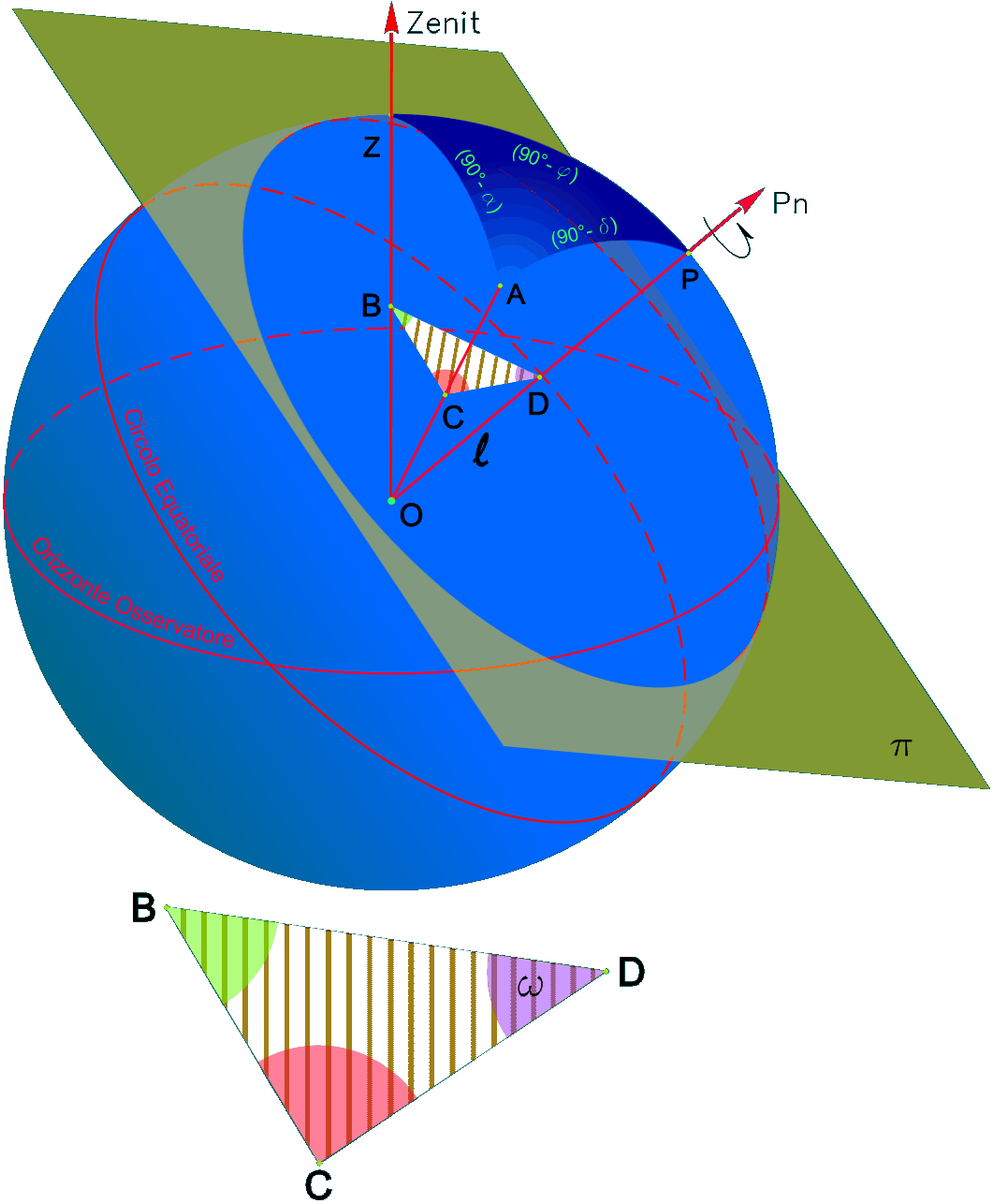  Ponendo OD = l si ha: 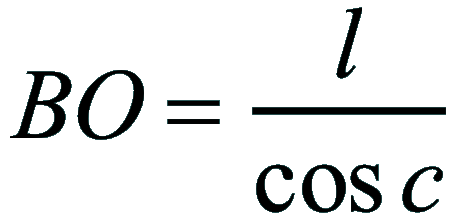 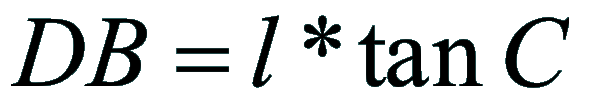 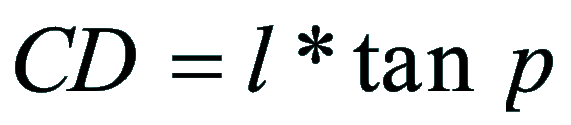 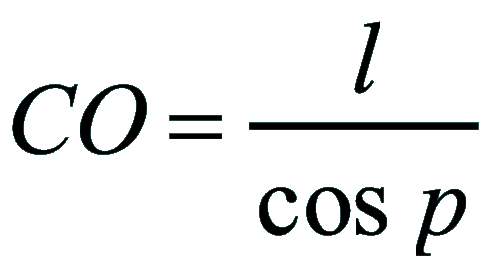 dal teorema del coseno: 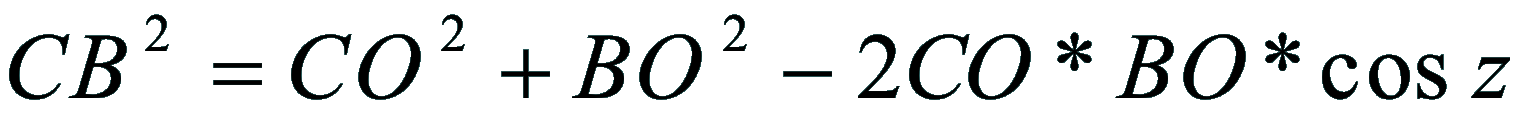 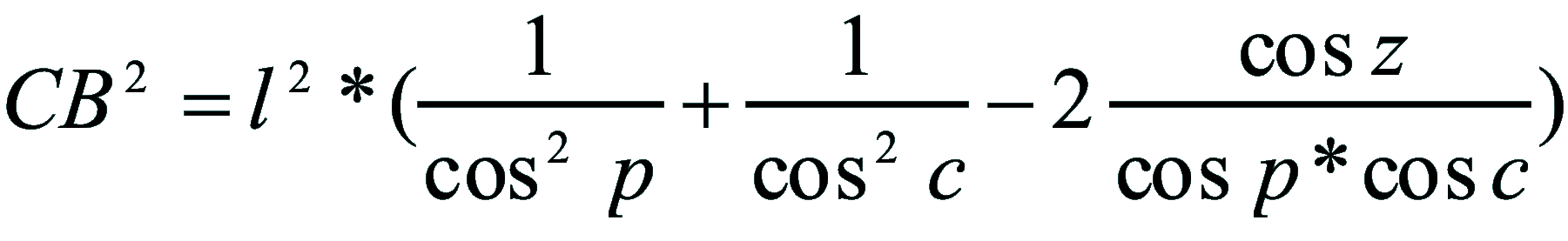 sul piano di sezione p risulta: 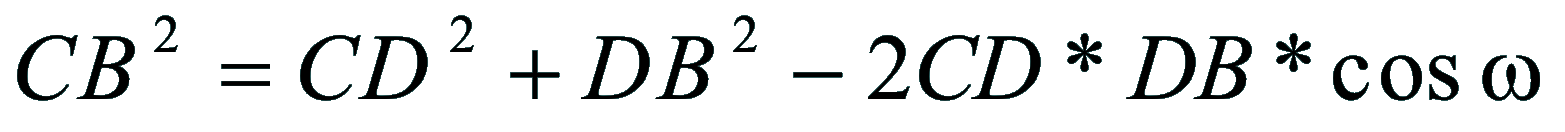 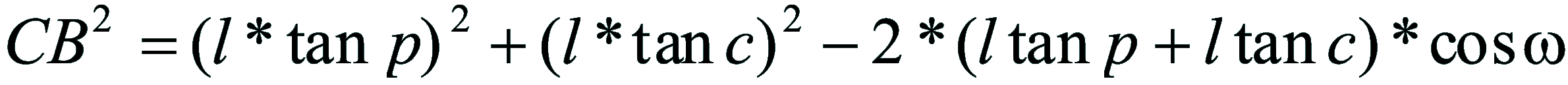 L'angolo orario w si misura sul piano ortogonale all'asse O-Pn 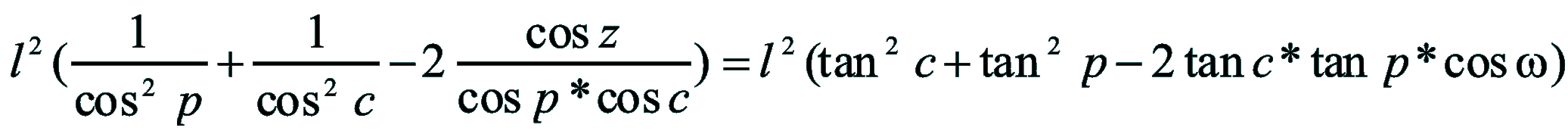 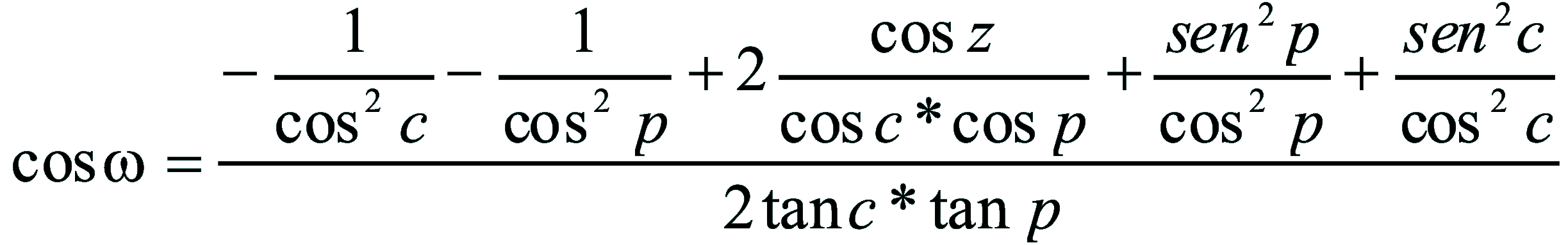 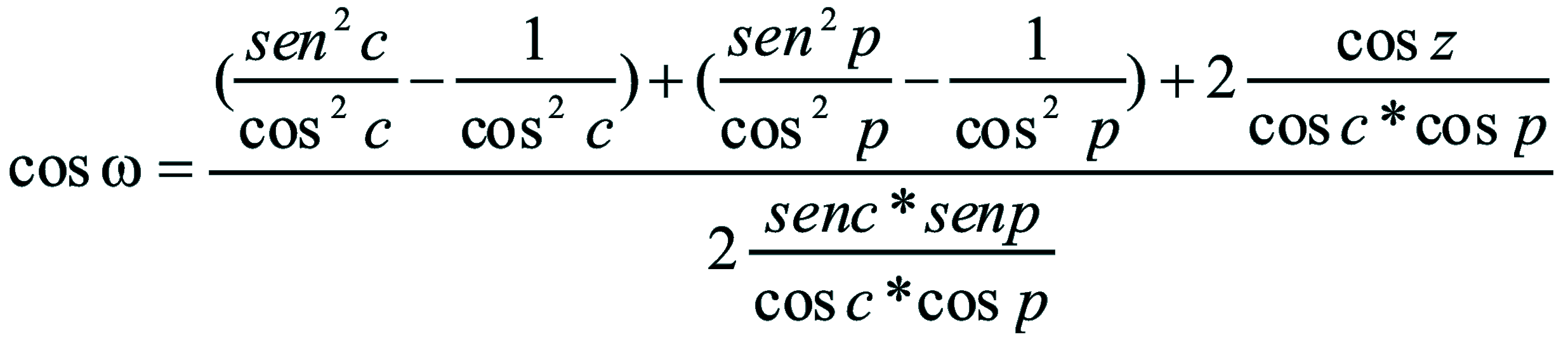 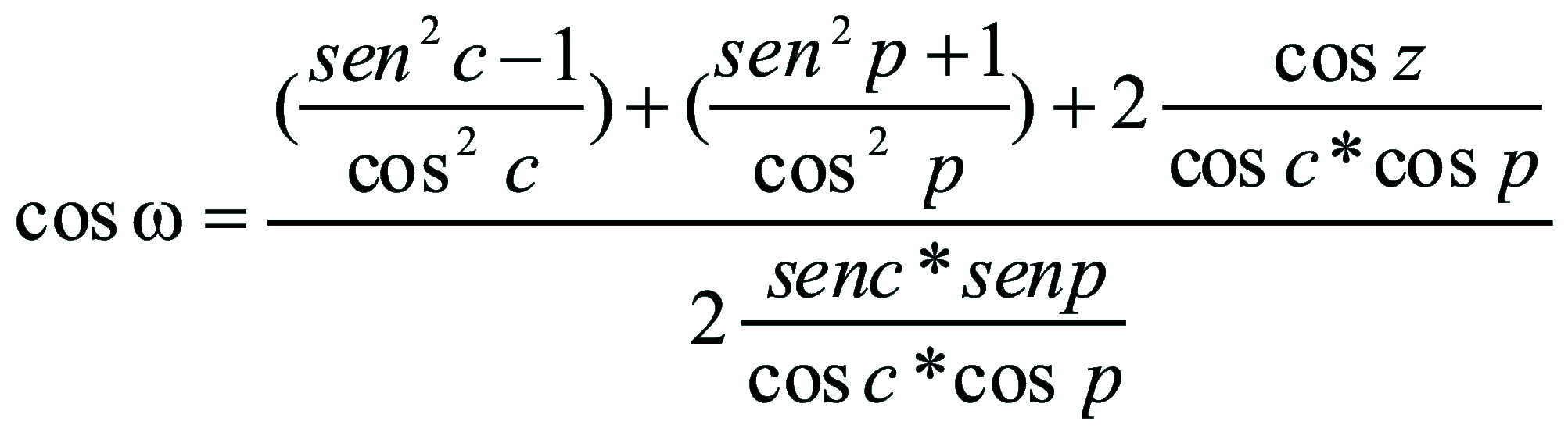 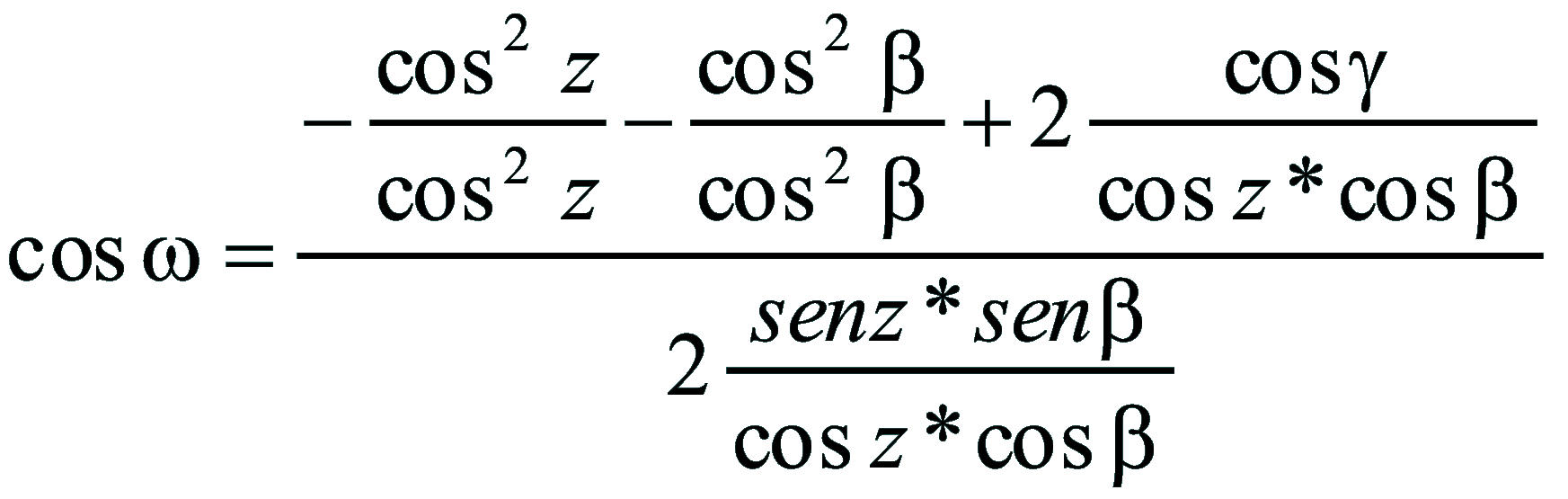 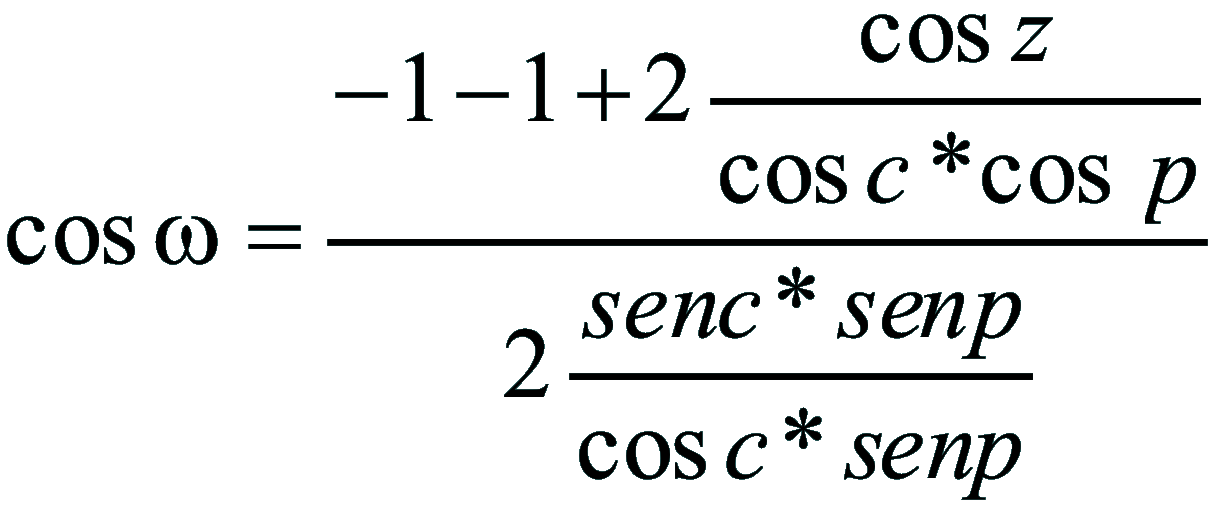 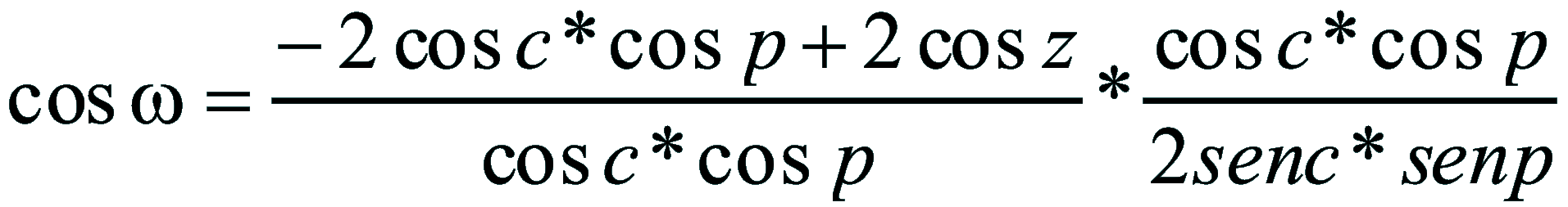 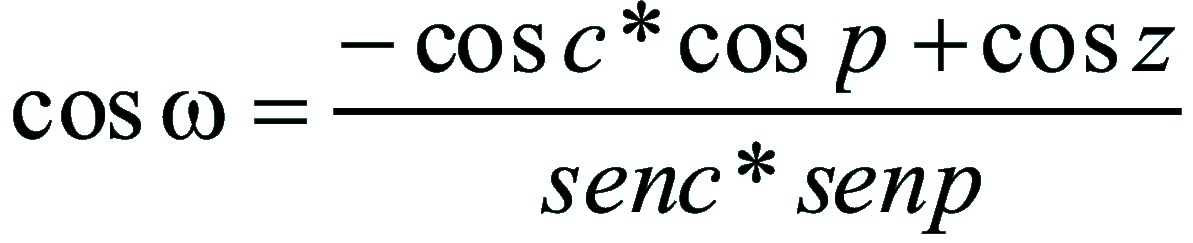 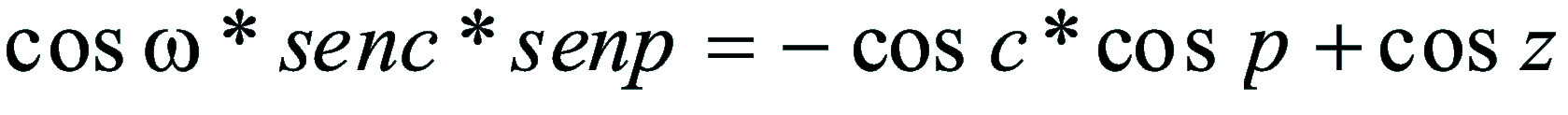 1) 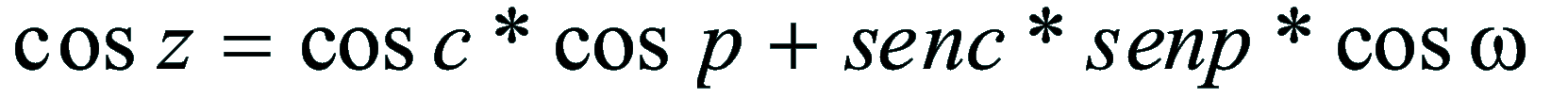  L'altezza α è l'arco di verticale del sole (90°) compreso fra l'orizzonte e il sole, contato da 0 a 90° dall'orizzonte verso lo Zenit e negativo dall'orizzonte al Nadir Per angoli complementari si ha: 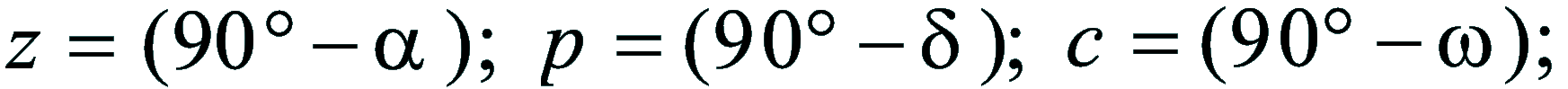 sostituendo nella 1) 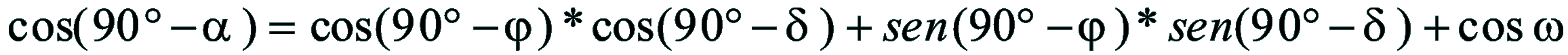 2) 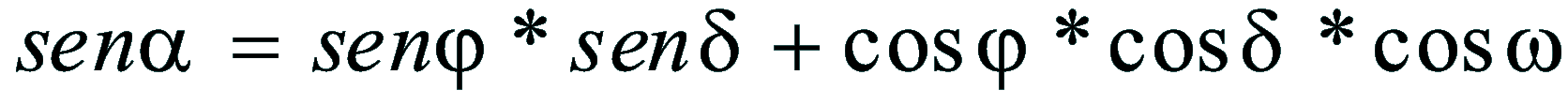 |  | Dimostrazione: Calcolo Azimut (b) Si considera un piano (п ) ortogonale all'asse polare OZ e si scompone il triedro sferico di posizione su un piano ortogonale a п passante per OB, e ponendo OB = l, si ha: 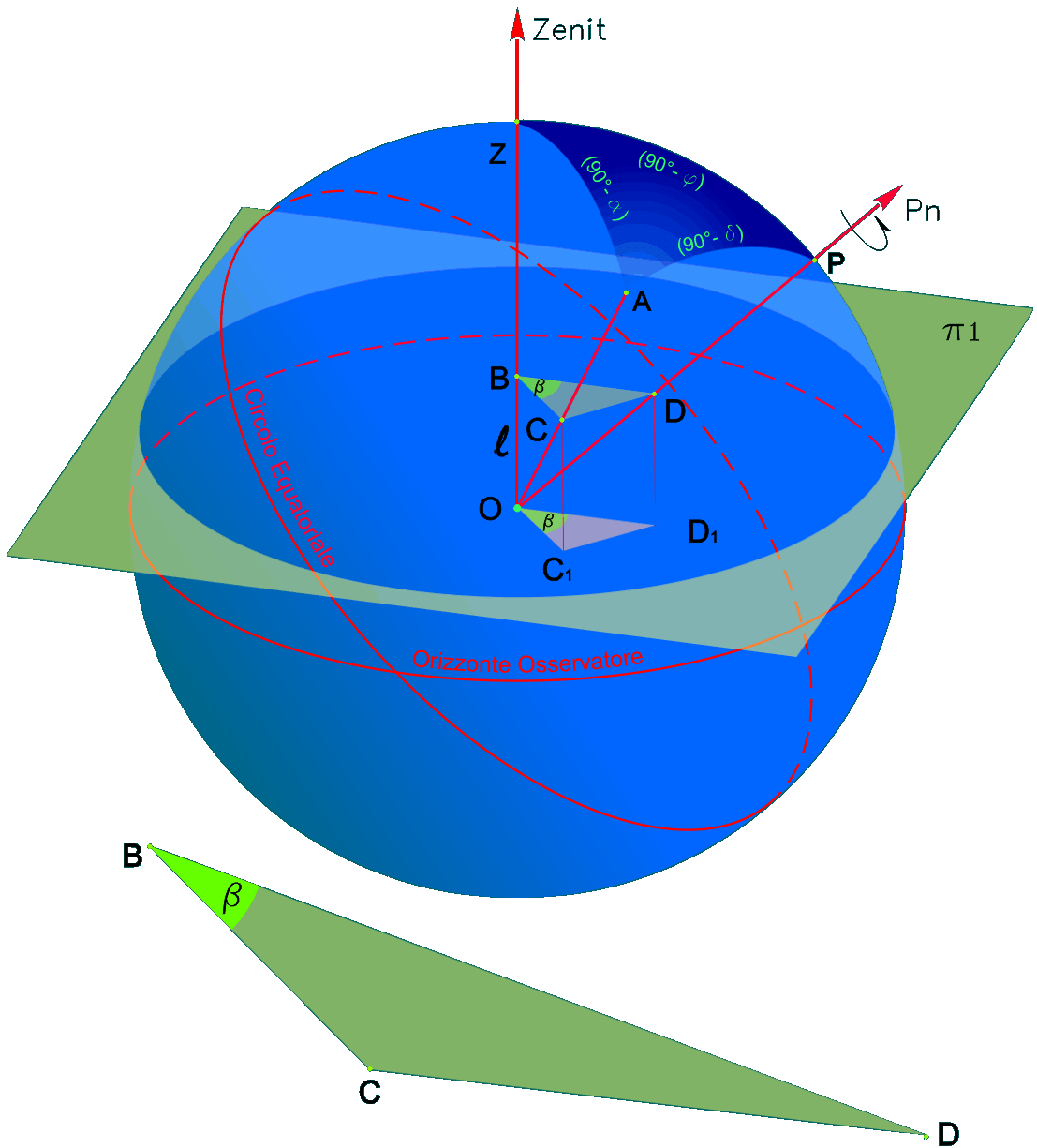 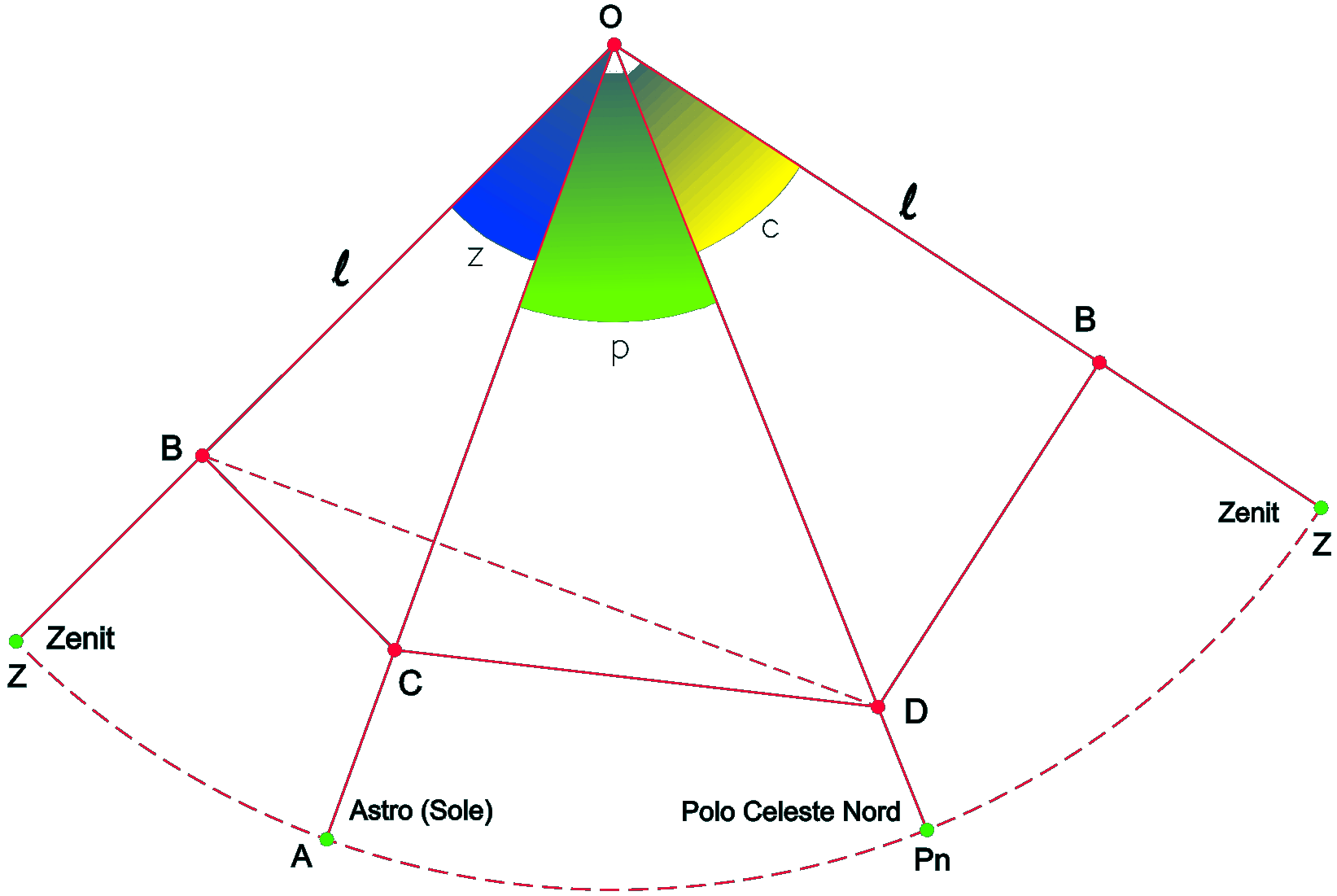 Dalla 2), che rappresenta la forma bruta del teorema di Eulero, è possibile calcolare l'altezza a di un astro (sole) rispetto all'orizzonte dell'osservatore conoscendo la Latitudine del luogo, la Declinazione del sole al tempo locale Tsl espresso attraverso l'angolo orario ω. 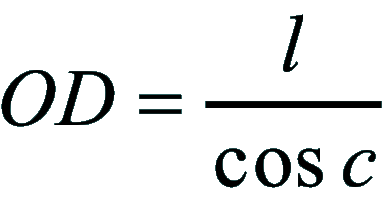   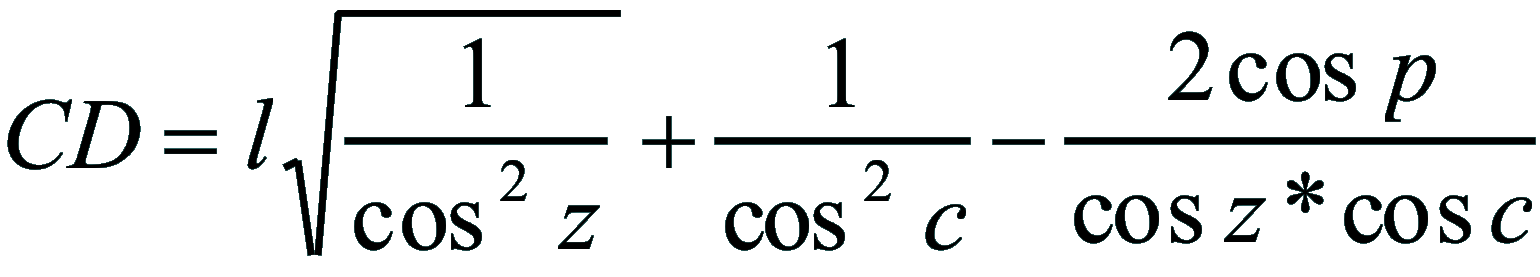 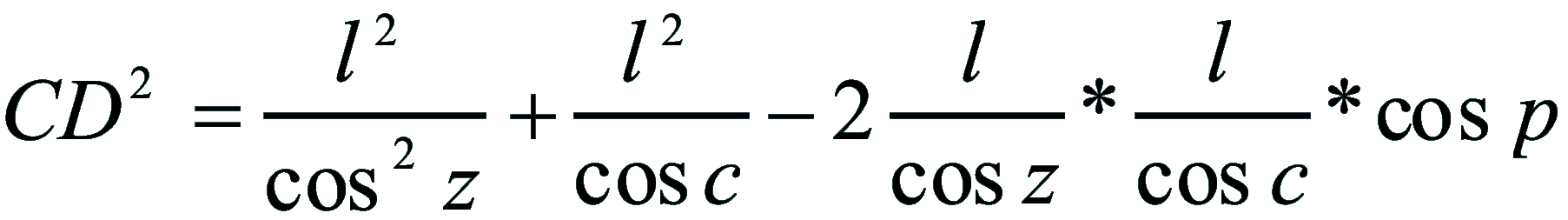 sul piano (п ) risulta: 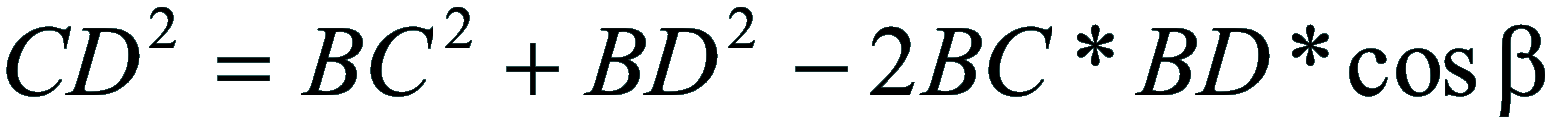 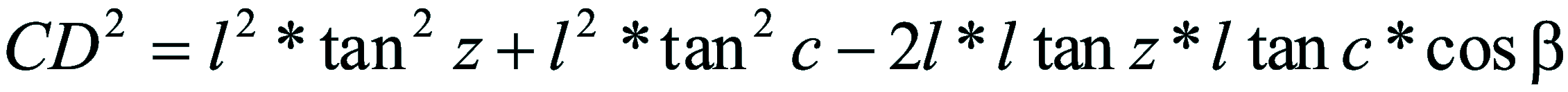 uguagliando i due termini: 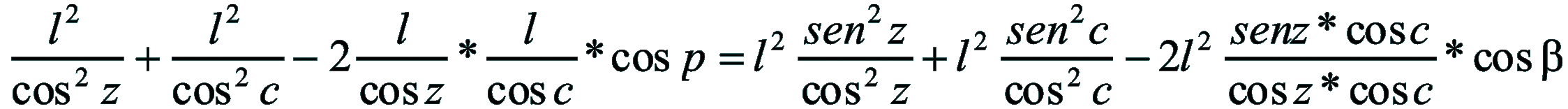 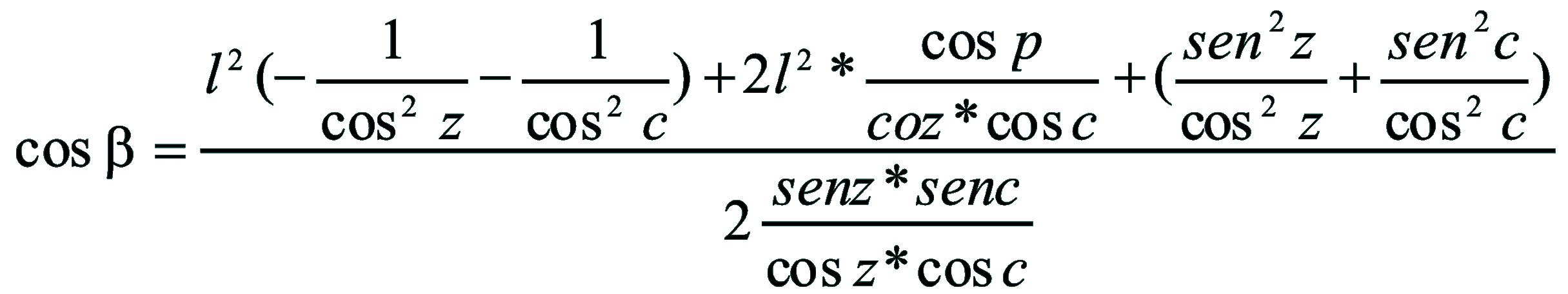 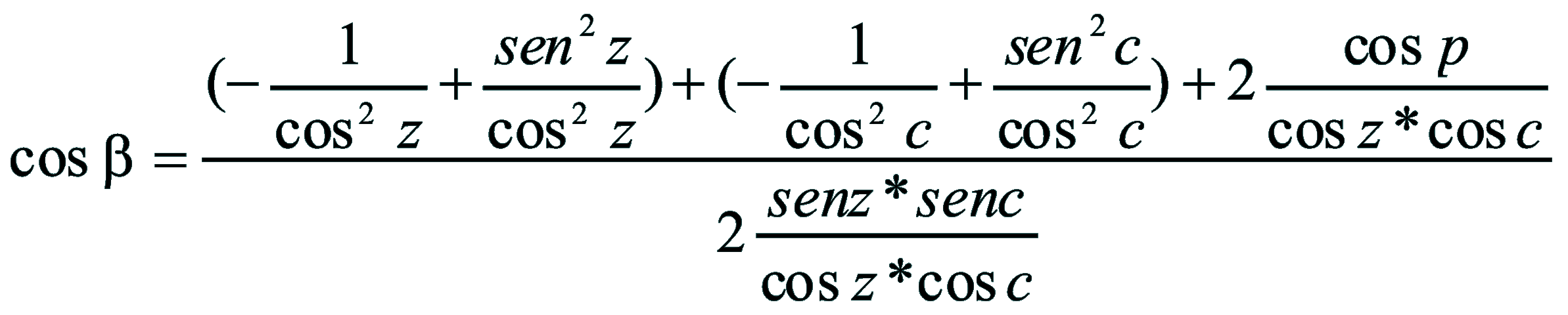 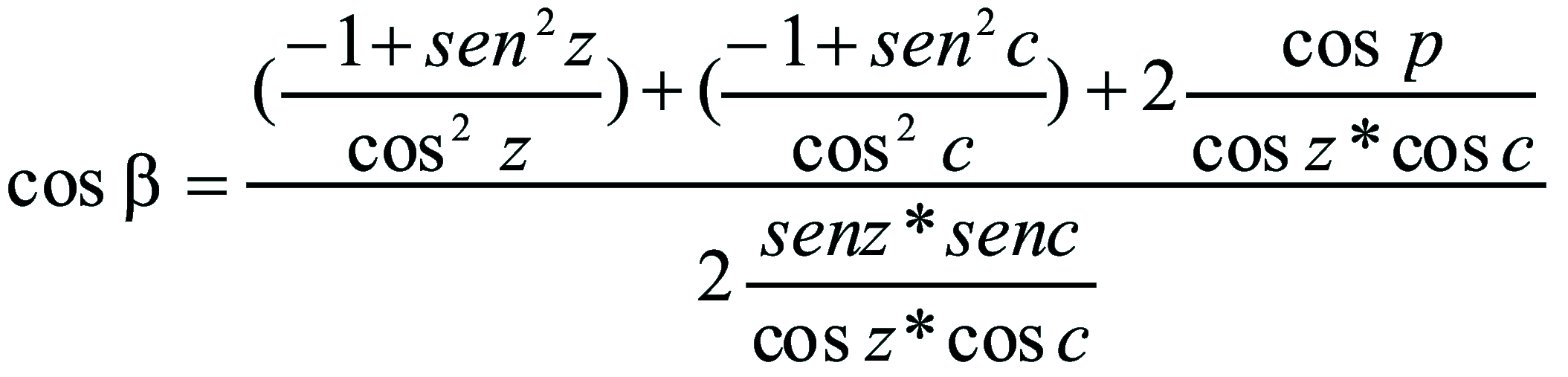 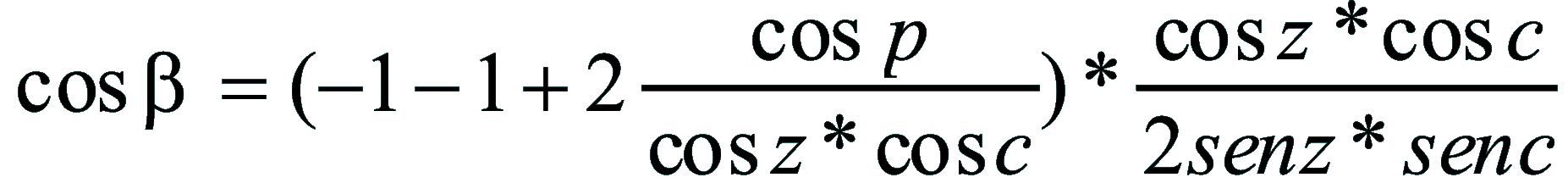 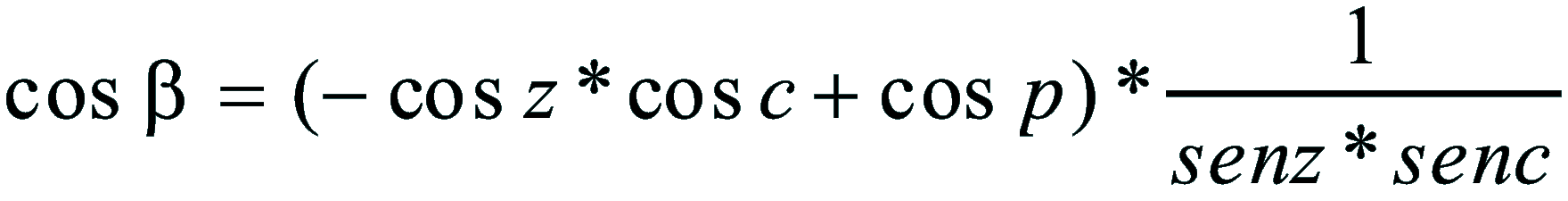 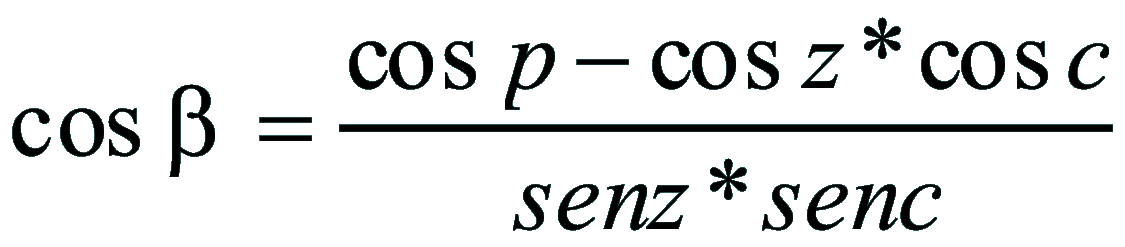 3) 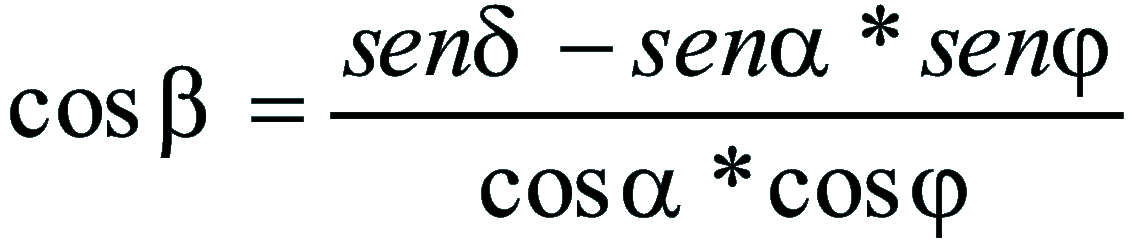 n alternativa alla 3) 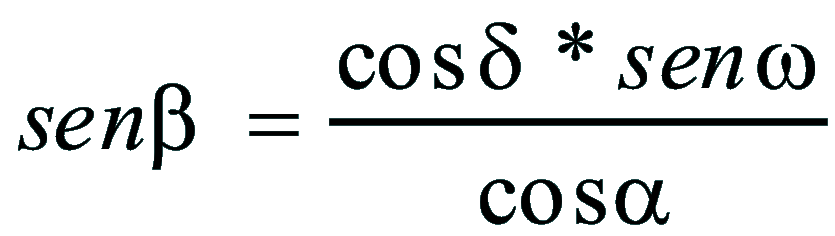 Per la costruzione delle carte solari si considera, come detto in precedenza, l'angolo formato dal meridiano astronomico dell'osservatore al circolo verticale del sole, misurato in senso antiorario o orario, nelle ore rispettivamente antimeridiane e pomeridiane. 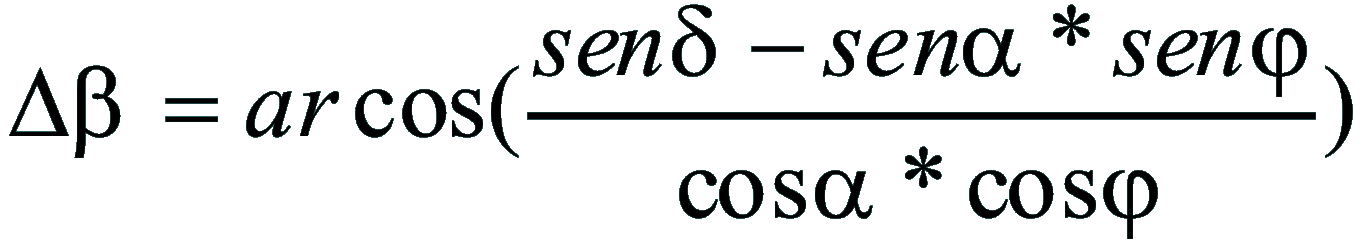 Declinazione δ La Declinazione δ di un astro (sole) è la distanza sferica dal piano dell'eclittica contato da 0 a 90° a partire dall'equatore ed è di specie Nord se l'astro si trova nell'emisfero Nord (Boreale), di specie Sud se l'astro si trova nell'emisfero Sud (Australe) . Poiché la declinazione δ dipende dal giorno si ha: formula di Cooper 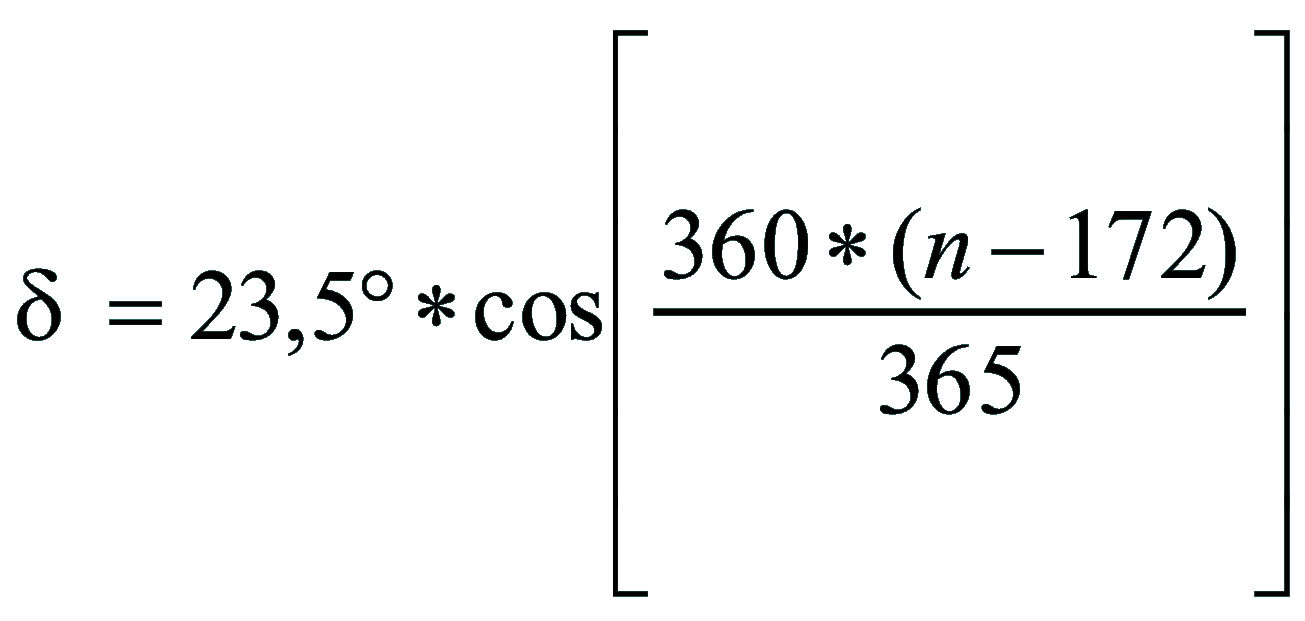 formula W.M.O. (Organizzazione Metereologica Mondiale) 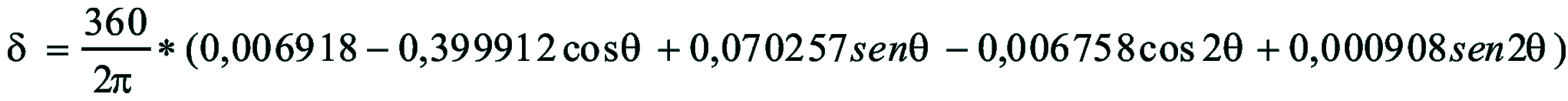 Nel secondo caso δ dipende da ө e da n (numero di giorni a partire dal 1° Gennaio n = 1)
Valori più precisi di declinazione possono essere trovati attraverso l'uso degli almanacchi relativi alle Effemeridi. * Corrado Brogi: Cenni di trigonometria sferica, pag. 61 |